Topologische Isolatoren
Das Keksdosen-Gleichnis
Ein topologischer Isolator lässt sich mit einer Keksdose aus Metall vergleichen, innen gefüllt mit isolierenden Keksen. Der elektrische Strom kann nur außen durch die metallische Dose fließen. Bei einem topologischen Isolator bestehen Dose und Kekse jedoch aus dem identischen Werkstoff.

Das Quantenrätsel
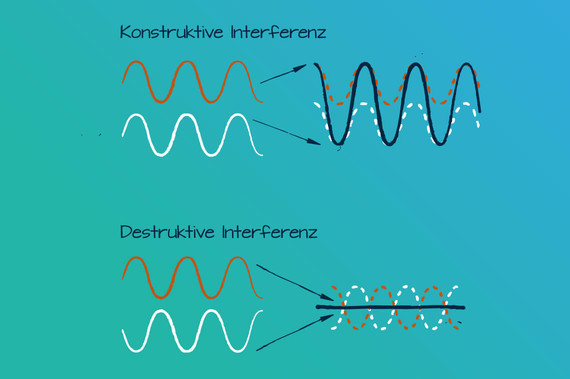
Mal Welle, mal Teilchen? Die geheimnisvolle Welt der Quanten unterscheidet da nicht so streng. Elektronen, die Basis moderner Chiptechnik, sind Quantenobjekte mit Welleneigenschaften. Überlagern sich Wellen, können sie sich gegenseitig verstärken oder auslöschen – konstruktive und destruktive Interferenz genannt.
Leiten oder isolieren?
Metalle wie Kupfer oder Gold sind gute elektrische Leiter. Glas oder Keramik wirken elektrisch isolierend. Diese Eigenschaften sind mit der Wellennatur der Elektronen im Material verknüpft. Die Mikroelektronik beruht darauf, spezielle Materialien gezielt von einem Strom leitenden in einen isolierenden Zustand zu schalten – oder umgekehrt. In Halbleitern werden die negativ geladenen Elektronenwellen an den elektrischen Feldern der Atomrümpfe des Kristallgitters gestreut und können sich überlagern, also interferieren. Durch das Anlegen einer Spannung ist einstellbar, ob diese Überlagerung konstruktiv (elektrisch leitend) oder destruktiv (isolierend) ist. Dies bildet die Grundlage für Computerchips. Die Elektronenwellen lassen sich aber noch viel präziser steuern.
Spektakulär! Der Quanten-Hall-Effekt
Extreme Präzision: 1980 entdeckte der Physiker Klaus von Klitzing, seinerzeit Privatdozent am Physikalischen Institut Würzburg, den Quanten-Hall-Effekt. Damit öffnete er das Tor zu einem neuen Gebiet der Festkörperphysik – und erhielt 1985 den Physik-Nobelpreis.
So entsteht der spektakuläre Effekt: Auf die Elektronen in einem Transistor wirkt von außen ein superstarkes Magnetfeld, 500.000-fach stärker als das Erdmagnetfeld. Ergebnis: Innen wird der Transistor zum Isolator, während Elektronenwellen mit perfekter Leitfähigkeit seinen Rand umlaufen. Noch außergewöhnlicher verhält sich die Hall-Leitfähigkeit: Sie ist quantisiert und beträgt exakt ein ganzzahliges Vielfaches der Größe e2/h (e = Elementarladung, h = Planck-Konstante) – auf 15 Stellen genau! Diese aufsehenerregende Präzision des neuen Quanteneffekts beruht auf den Prinzipien der Topologie, einem Teilgebiet der Mathematik.

Topologischer Isolator: Er funktioniert!
Der Quanten-Hall-Effekt wird durch ein superstarkes Magnetfeld kontrolliert – ungeeignet für praktische Anwendungen im Alltag. Deshalb wurde lange nach ähnlichen Effekten gefahndet, die ohne Magnetfeld funktionieren. Der Durchbruch kam 25 Jahre später: Am Lehrstuhl für Experimentelle Physik 3 der Universität Würzburg wurde die elektrische Leitfähigkeit von Quecksilber-Tellurid (HgTe) untersucht. Dabei traten Eigenschaften zutage, die mit herkömmlichen Modellen nicht erklärbar waren. Ein weltweiter Forschungsboom begann, als Professor Laurens W. Molenkamp und seinem Team 2007 der weltweit erste experimentelle Nachweis eines topologischen Isolators gelang.
Quantenphysik trifft Einstein
Neben der elektrischen Ladung besitzen Elektronen auch ein magnetisches Moment, Spin genannt. Der Spin wird durch Magnetfelder beeinflusst und spielt überraschenderweise auch dann eine Rolle, wenn gar kein äußeres Magnetfeld angelegt wird! Nach der Einstein’schen Relativitätstheorie nimmt der Spin die elektrischen Felder im Kristall nämlich als effektive Magnetfelder wahr, wenn sich die Elektronen durch das Kristallgitter bewegen. Durch geschicktes Maßschneidern von Material und Kristallgitter lässt sich dieses Phänomen nutzen, um isolierendes Verhalten im Inneren und perfekt leitende Ränder zu erzeugen – wie beim Quanten-Hall-Effekt. Ein starkes äußeres Magnetfeld ist also unnötig, denn die Elektronen bringen ihr eigenes mit.
Dieses Konzept des topologischen Isolators schlugen Charles L. Kane und Eugene J. Mele erstmals 2005 für Graphen vor, ein Honigwabengitter aus Kohlenstoffatomen. Allerdings erwies sich Graphen für den experimentellen Nachweis topologischen Verhaltens als wenig geeignet. Für Lichtwellen funktioniert diese Geometrie jedoch sehr gut.
Ohne Widerstand
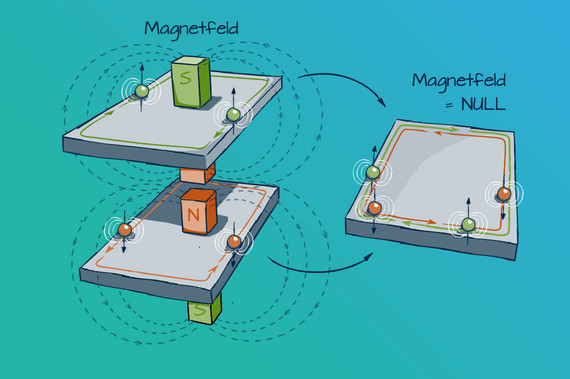
Der Quanten-Spin-Hall-Effekt ist vergleichbar mit zwei Kopien des Quanten-Hall-Effekts für jeweils entgegengerichtete Magnetfelder. Bei der Addition beider Zustände kompensieren sich die Magnetfelder, sie gleichen sich also aus. Dabei entstehen zwei gegeneinander laufende Randleitungszustände mit entgegengesetzter Spin-Ausrichtung. Letzteres bewirkt, dass beide Kanäle widerstands- bzw. verlustfrei einen ungehinderten gegenläufigen Stromfluss ermöglichen. Dies geschieht allein aufgrund der inneren Struktur des Materials, egal wie präzise der Rand gestaltet ist. Denn in der Topologie ist ein Rand immer ein Rand, ganz gleich, wie krumm oder ausgefranst er ist.
Rechnen mit Spins
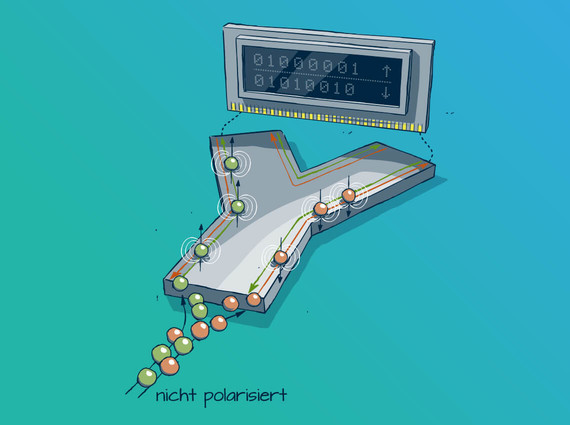
Mithilfe des Quanten-Spin-Hall-Effekts (QSHE) sind ohne Einsatz externer Magnetfelder neuartige elektronische Bauelemente möglich, die mit Elektronen-Spins rechnen. Die Abbildung zeigt, dass der QSHE genutzt werden kann, Elektronen entsprechend ihres Spins zu trennen.
Diese Anordnung eignet sich sowohl zur Erzeugung spin-polarisierter Ströme als auch zu deren Analyse, da nur Spins einer Sorte entlang eines Kanals (rot oder grün) fließen können. Ohne Einsatz externer Magnetfelder lassen sich Informationen magnetisch kodieren, transportieren und sich so für Spin-Transistoren nutzen – das ist Spintronik.