Was lässt sich noch alles um die Ecke schicken? Schau’s dir an!
Topologisch geschützte Wellen gibt es in vielen Varianten. Selbst am Äquator kann man ihnen begegnen. Die Forschungen zu diesem Thema sind sehr vielfältig, die möglichen Anwendungen faszinierend. So könnten etwa die „Topocoustics“ – eine Symbiose aus Topologie und Akustik – künftig zum Beispiel zu speziell konstruierten Schutzwänden führen, die Schallwellen so (um-)lenken, dass der Lärm der Umgebung absorbiert wird.
Topologie: global betrachtet
Die Topologie hilft, das Innere von Quantenmaterialien zu erklären. Sie ist ein Teilgebiet der Mathematik und befasst sich mit den globalen Eigenschaften geometrischer Gebilde, die unter stetiger Verformung erhalten bleiben. Ein Wirbelsturm wächst zum Beispiel zu einem Hurrikan, ohne seine Drehrichtung zu ändern. Die Drehrichtung ist eine topologische Eigenschaft.
Topologisch geschützt heißt, dass Änderungen an den Parametern eines Systems die jeweils geschützte Eigenschaft nicht beeinflussen. So ist in der Topologie ein Rand immer ein Rand, ganz gleich, wie krumm er ist. Bei einem topologischen Isolator beispielsweise ist die praktisch widerstandsfreie Leitfähigkeit auf seiner Oberfläche bzw. am Rand die topologisch geschützte Eigenschaft. Das Innere hingegen verhält sich wie ein Isolator und leitet keinen Strom.
Der Forschung an topologischen Materialien widmet sich das Würzburg-Dresdner Exzellenzcluster ct.qmat – Complexity and Topology in Quantum Matter (Komplexität und Topologie in Quantenmaterialien). Das Exzellenzcluster wird im Rahmen der Exzellenzstrategie des Bundes und der Länder gefördert.
Perfekte Welle am Äquator
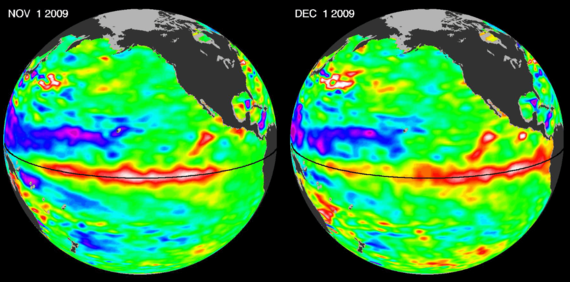
Erde mit überlagerter Äquatorialwelle. Abbildung aus: Venaille, A., Delplace, P. Topological waves in geophysical fluids. (2018) URL: https://physics-complex-systems.fr/wp-content/uploads/2017/11/M2_sujet_GFDtopo_english.pdf (abgerufen am 23. Februar 2021; © NASA/JPL-Caltech)
Sogar die Weltmeere zeigen topologische Erscheinungen. Genauer gesagt geht es dabei um die ausgedehnten Wellen entlang des Äquators mit Wellenlängen von mehreren hundert bis tausend Kilometern. Weil sich Hurrikans und Meereswirbel auf der Nordhalbkugel immer in die gleiche Richtung und genau entgegengesetzt zu jenen auf der Südhalbkugel drehen, entsteht genau am Äquator eine stabile „Randwelle“. Daraus ergeben sich an dieser Grenze zwischen Nord- und Südhalbkugel topologische Effekte, aus denen sich zum Beispiel das El-Niño-Ereignis erklärt: Diese etwa alle vier Jahre wiederkehrende warme Meeresströmung an den Küsten Südamerikas lässt sich weder durch Stürme noch durch Inseln stören – denn sie ist topologisch geschützt.
Weiterlesen?
- Geophysical WavesVideos und Erläuterungen
- Delplace, P., Marston, J. B., Venaille, A. Topological origin of equatorial waves. Science 358, 1075-1077 (2017). DOI: 10.1126/science.aan8819
Unsere Ohren empfangen Schallwellen. Das ist Normalität – und Stille heutzutage eher selten. Doch was, wenn man Lärm einfach um die Ecke leiten und so eine Insel der vollkommenen Ruhe schaffen könnte? Für einzelne Frequenzen – gemeint sind reine Töne wie die aus einer Stimmgabel – lässt sich das mit einem Honigwabengitter aus kleinen Hohlräumen erreichen, wie in der Abbildung zu sehen.
Der Schall läuft hier ausschließlich in den kleinen Kammern außen entlang. Eine in der Mitte sitzende Person wäre demnach vor dem entsprechenden Ton geschützt, weil sich die Wellen dort gegenseitig auslöschen. Ein eingebautes Noise-Cancelling sozusagen, um unerwünschte Geräusche zu reduzieren. Diese Forschungsrichtung nennt sich „Topocoustics“ – zusammengesetzt aus den Begriffen Topologie und Akustik – und könnte in Zukunft zu neuartigen Schallschutzwänden oder verbesserten Tonstudios führen.

Wabenstruktur, die den Schall „um die Ecke schickt“: Experimenteller Aufbau eines hexagonalen akustischen Gitters am Physikalischen Institut der Julius-Maximilians-Universität Würzburg.
Fotos: F. Hoffmann/S. Widmann, Experimentelle Physik VII, Julius-Maximilians-Universität (JMU) Würzburg, 2020

Rastertunnelmikroskopie-Aufnahme von Bismuten sowie schematische STM-Darstellung. Foto: Universität Würzburg; Lehrstuhl Experimentelle Physik 4 / Skizze: Wikipedia (Thorsten Feichtner)
An der Julius-Maximilians-Universität (JMU) Würzburg werden die topologischen Eigenschaften verschiedener Materialien untersucht. Wird eine Einzellage Bismut-Atomeauf den Halbleiter Siliziumcarbidaufgedampft, bilden diese Bi-Atome ein Honigwabengitter. So entsteht hier ein topologischer Isolator namens Bismuten, in dem sich die Elektronen nur am Rand bewegen können. Die Würzburger Wissenschaftler:innen können diese Elektronen jetzt sehr direkt erforschen, indem sie mit der dünnen, feinen Spitze eines Rastertunnelmikroskopsüber das Material „tasten“ (Scanning Tunneling Microscopy STM). Das Resultat sind eindrucksvolle Bilder in atomarer Auflösung, die zeigen, wie sich die an der Außenkante zusammengepferchte Elektronen gegenseitig im Weg stehen können. Bei tiefen Temperaturen vermindern sie ihre Geschwindigkeit, um Zusammenstöße zu vermeiden. Ein Verhalten, das bei normalen Metallen nicht zu beobachten ist. Wenn sich Elektronen nur am Rand eines Materials befinden, wird das als „Tomonaga-Luttinger-Verhalten“ bezeichnet.
Weiterlesen?
- JMU Würzburg: „Topologische Isolatoren: Elektronen halten Sicherheitsabstand“
- Stühler, R., Reis, F., Müller, T. et al. Tomonaga–Luttinger liquid in the edge channels of a quantum spin Hall insulator.Nat. Phys. 16, 47–51 (2020). https://doi.org/10.1038/s41567-019-0697-z
- Freie Version der Fachpublikation „Tomonaga–Luttinger liquid ...“in arXiv
Die mathematischen Prinzipien der Topologie lassen sich ebenso auf photonische Systeme anwenden. So wurden topologische Isolatoren für Licht in gekoppelten optischen Wellenleitern realisiert. Diese synthetischen Medien können das Licht dazu bringen, sich vollkommen streufrei in einer vorgegebenen Richtung entlang des Rands auszubreiten und sich dabei nicht einmal von einer Ecke aufhalten zu lassen.
Photonenunterscheiden sich dabei fundamental von den Elektronen, die in festkörperbasierten topologischen Isolatorenfließen: Deren zwei wohldefinierte Spin-Zustände„Up“ und „Down“ gibt es in der Optik nicht. Die überaus nützliche Spin-Eigenschaft lässt sich jedoch durch eine geschickte Vernetzung der Wellenleiter simulieren.
Ergebnis ist, dass am Rand eines optischen Systems nicht nur ein, sondern zwei robuste und streufreie Pfade für Licht existieren, die sich trotz ihrer entgegengesetzten Ausbreitungsrichtungen nicht gegenseitig stören. Die Photonen verhalten sich hier also wie Spin-polarisierte Elektronen.
Photonische topologische Isolatoren sind dabei weitaus mehr als ein geschickter Nachbau elektronischer Systeme. Dank hochintensiver Laser eröffnen sie vollkommen neue Anwendungsszenarien – denn „mehr Licht“ ist nicht nur heller, sondern kann sich auch gänzlich anders verhalten, als man es auf den ersten Blick erwarten würde. Grund dafür sind nichtlineare Effekte, bei denen ein stark angeregtes System grundlegend anders verhält als bei schwacher Anregung. Somit können sich intensive Lichtpulse sogar ihre ganz eigene topologische Umgebung definieren, und diese schützende Hülle auf ihrem Weg durch das ansonsten unscheinbare Wellenleiternetzwerk mitführen.
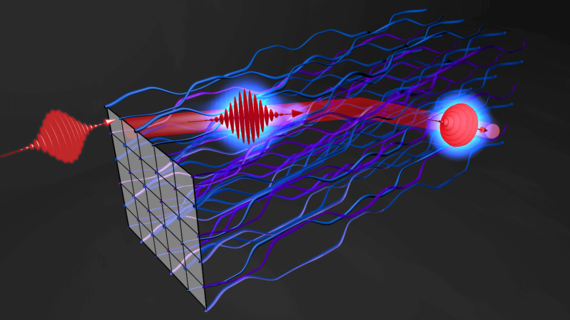
Abbildung: Ein nichtlinearer topologischer Isolator für Licht. Intensive Laserpulse erschaffen eine schützende Hülle, die sie vor Streuung und äußeren Störeinflüssen schützt.
Danke für die inhaltliche Unterstützung an Prof. Dr. Alexander Szameit, Lukas J. Maczewsky, Arbeitsgruppe Experimentelle Festkörperoptik, Institut für Physik, Universität Rostock.
Weiterlesen?
- Universität Rostock: „Quantenoptiker zwingen Lichtteilchen, sich wie Elektronen zu verhalten“
- Maczewsky, L. J., Höckendorf, B., Kremer, M. et al. Fermionic time-reversal symmetry in a photonic topological insulator. Nat. Mater. 19, 855–860 (2020). https://doi.org/10.1038/s41563-020-0641-8
- Maczewsky, L. J., Heinrich, M., Kremer, M. et al. Nonlinearity-induced photonic topological insulator. Science 370, 701-704 (2020).
https://doi.org/10.1126/science.abd2033 - Freie Versionen der Fachpublikation in arXiv:
„Fermionic time-reversal symmetry ...“
„Nonlinearity-induced photonic topolgical insulator“

Darstellung eines Gitters miteinander gekoppelter Mikrokavitäten (Halbleiterbauelemente), in deren Mitte Quantenfilme (rot) integriert wurden. Die Geometrie entspricht einer Honigwabenstruktur und wird als polaritonisches Graphen bezeichnet. Abbildung: Karol Winkler, Technische Physik, Julius-Maximilians-Universität Würzburg
Die Quantenmechanikbietet etliche Überraschungen fernab jeder Alltagserfahrung. Nicht nur Materie (Elektronen) oder Licht (Photonen) sind Welle und Materie gleichzeitig – es gibt sogar Hybride aus Materie und Licht. Die Mischzustände heißen Exziton-Polaritonen.
Diese Teilchen befinden sich in einem Gitter aus Halbleiter-Mikroresonatoren (siehe nebenstehende Abbildung). Das sind kleine Laser, von denen jeder einzelne einen geringeren Durchmesser hat als ein menschliches Haar. Diese Mikroresonatoren sind angeordnet wie ein Honigwabengitter – genauso wie die Kohlenstoffatome in einer Graphenschicht.
Video: Um die Ecke geschickt – eine Simulation
Durch Laseranregung und ein starkes Magnetfeld konnten in diesem Gitter erstmals topologische Randeffekte für Exziton-Polaritonen nachgewiesen werden.
Im Film ist eine Simulation von Exziton-Polaritonen in einer topologischen Isolatorstrutkur zu sehen. Die Teilchen passieren mehrere Ecken, ohne gestreut zu werden. Die hybriden Licht-Materie-Teilchen bewegen sich entlang des Rands dieser Struktur und um die Ecken, ohne zurückgestreut zu werden oder in das Volumen einzudringen.
Film: Dr. Oleg Egorov, Institut für Festkörpertheorie und -optik, Friedrich-Schiller-Universität Jena
Weiterlesen?
- pro-physik.de: „Ein topologischer Isolator für Exziton-Polaritonen“
- Klembt, S., Harder, T.H., Egorov, O.A. et al. Exciton-polariton topological insulator.Nature 562, 552–556 (2018). https://doi.org/10.1038/s41586-018-0601-5
- Freie Version der Fachpublikation „Exciton-polariton topological insulator“in arXiv

